Uwaga dla czytających w formie newslettera: objętość publikacji przekracza limit Gmaila (innych skrzynek mailowych zapewne też) – by poprawnie wyświetlić tekst oraz wszystkie ilustracje, otwórz artykuł bezpośrednio na Substack.
Dla wygody mobilnego czytania, polecam również wypróbować aplikację na telefon:
Read TexasBocaChica (PL) in the Substack app
Available for iOS and Android
Śledząc rozwój sektora kosmicznego trudno nie zetknąć się ze specjalistyczną terminologią. Co ma na myśli Musk mówiąc, że zmiany w projekcie pozwolą osiągnąć większe ∆v? Czym jest impuls właściwy i dlaczego z powodu tego parametru Starship potrzebuje silników o małych i dużych dyszach? Jak międzyplanetarna sonda zyskuje prędkość, nie zużywając przy tym grama paliwa?
Odpowiadając na te i inne pytania, tekst ma na celu zapewnienie obserwatorom postępów prac w teksańskim Starbase, a także entuzjastom rakiet wszelakich, lepszego zrozumienia kluczowych koncepcji z zakresu inżynierii rakietowej oraz mechaniki orbitalnej.
Masa i jej rozpędzanie
Zdrowy rozsądek podpowiada, że większa masa oznacza konieczność spalenia większej ilości paliwa, by osiągnąć dany cel czy daną prędkość – pod tym względem, analogia chociażby z samochodem wydaje się w pełni poprawna.
Załadowana ciężarówka potrzebuje potężniejszego silnika oraz więcej litrów paliwa niż motocykl, by rozpędzić się do 100 km/h. Idąc tym tokiem rozumowania szybko dojdziemy jednak do wniosku, że porównanie z pojazdami kołowymi przestaje być adekwatne: jeśli chcemy zatrzymać samochód wystarczy, że zdejmiemy nogę z gazu na odcinku prostej drogi. W przypadku statku kosmicznego, brak „nogi na gazie” nie spowoduje jego zatrzymania – przestrzeń kosmiczna nie spowalnia raz rozpędzonych obiektów.
Ten prosty fakt oznacza, że chcąc określić maksymalny zasięg statku, nie ma sensu, w przeciwieństwie do samochodu czy samolotu, posługiwać się kilometrami. Wysłana w przestrzeń sonda może bowiem przemierzyć ich nieskończenie wiele, jeśli nic jej nie zatrzyma; a wytracenie prędkości w próżni również odbywa się kosztem spalania paliwa – dokładnie taka samo, jak przy jej zwiększaniu.
W podróżach kosmicznych najważniejsze jest więc, jak duża zmiana prędkości konieczna jest do osiągnięcia celu.
Delta-v
W planowaniu misji, inżynierowie posługują się parametrem zwanym delta-v (w fizyce delta wyraża zmianę, v to prędkość), wyrażanym najczęściej w kilometrach lub metrach na sekundę.
Poniższa mapa przedstawia wybrane obiekty Układu Słonecznego wraz z niezbędnym do osiągnięcia kolejnych „stacji” przyśpieszeniem.
Jak czytać mapę? Chcąc ustalić wartość przyśpieszenia koniecznego do osiągnięcia celu (np. niskiej orbity Księżyca lub powierzchni Europy, lodowego satelity Jowisza) należy zsumować podaną kolorem niebieskim delta-v na wybranym odcinku trasy. Liczby podane są przy założeniu efektywnej orbity transferowej, czyli tzw. transferu Hohmanna; czerwone strzałki na mapie oznaczają możliwość hamowania w atmosferze danego ciała [Autor mapy: u/CuriousMetaphor via Reddit.com]
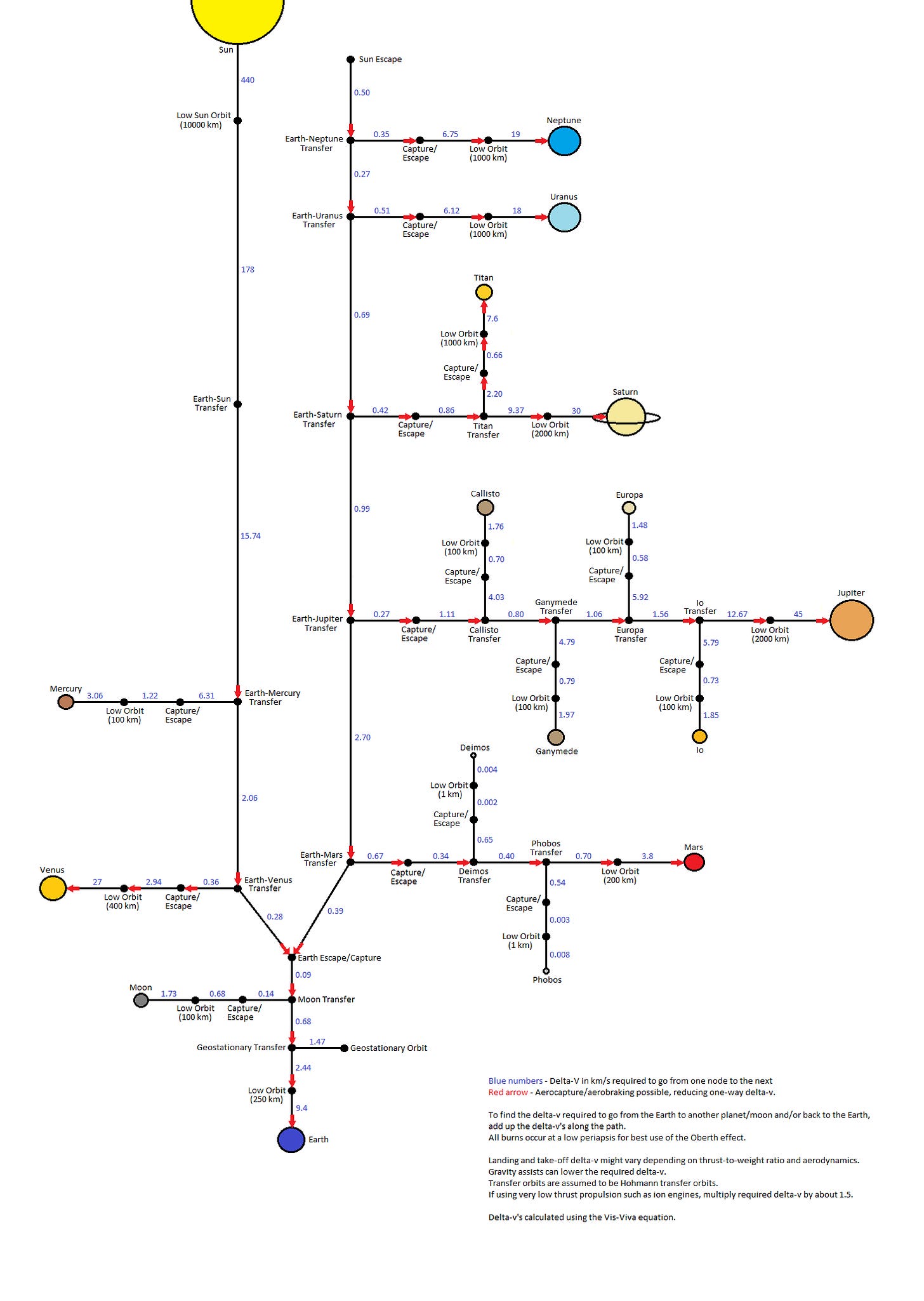
Należy przy tym pamiętać, iż przez przyśpieszenie w fizyce rozumiemy również spowolnienie (będące po prostu przyśpieszeniem o przeciwnym zwrocie) czy zmianę kierunku (przyśpieszenie „w bok”) – każdy taki manewr w kosmosie musi być uwzględniony w kalkulacji delta-v dla danej misji1.
Gdy mówimy, że sonda potrzebuje do zajęcia orbity wokół ciała niebieskiego danego delta-v, mamy na myśli sumę wszystkich manewrów, które musi ona wykonać.
Z kolei mówiąc o „budżecie delta-v” wskazujemy, jakie manewry sonda jest fizycznie w stanie wykonać, zanim zużyje swoje paliwo (występuje tu pewna analogia do wskaźnika rezerwy w samochodzie).
W praktyce lotów kosmicznych, delta-v jest miarą tożsamą* ze zmianą orbity – np. zajęcie wyższej, stabilnej orbity wokół Ziemi musi wiązać się ze zużyciem paliwa, a zatem redukuje dostępny dla danego statku „limit” delta-v na kolejne manewry. To, jaką delta-v dysponuje statek o określonym zapasie paliwa, determinowane jest przez stosunek ciągu do masy statku oraz efektywność jego silników.
*a właściwie tożsamą „jednostronnie”, gdyż możliwym jest skierowanie statku na inną orbitę bez „uszczuplania” budżetu delta-v(o tym za chwilę), lecz wygenerowanie ciągu zawsze oznacza zmianę prędkości, a tym samym orbity.
Większy budżet delta-v można uzyskać na drodze:
odrzucania stopni/pustych zbiorników paliwa (czy dowolnej innej redukcji masy – rakieta Electron firmy Rocket Lab odrzuca np. rozładowane baterie, zasilające turbiny pomp);
poprawienia proporcji masy statku do masy paliwa;
użycia silników o większym impulsie właściwym;
[jeśli liczyć z uwzględnieniem startu z ciała niebieskiego] osiągnięcia prędkości orbitalnej, czyli tzw. pierwszej prędkości kosmicznej, w krótszym czasie (minimalizacja straty na skutek grawitacji, ang. gravity loss).
Dwa pierwsze sposoby wydają się naturalne – lżejszy statek przyśpieszyć jest oczywiście łatwiej.
Metoda trzecia i czwarta wprowadzają kolejne, specjalistyczne pojęcia z dziedziny inżynierii (nie tylko rakietowej), wymagające wyjaśnienia.
Za punkt wyjścia przyjmiemy trzecią zasadę dynamiki Newtona, czyli zasadę zrównującą siłę, towarzyszącą każdej akcji, z przeciwnie skierowaną reakcją. W jej myśl, kluczowymi parametrami dla rozpędzenia rakiety są:
sumaryczna masa cząstek, które wydostają się przez dyszę silnika
prędkość oraz kierunek cząstek opuszczających silnik.
Zmienne w postaci masy i prędkości nie powinny sprawiać nikomu problemu – logika wskazuje, że jeśli dwa silniki wyrzucają w tym samym kierunku cząstki o równej masie x, to większy ciąg wygeneruje ten silnik, który przyśpieszy cząstki do większej prędkości (akcja = reakcja).
Impuls właściwy (ISP)
Przez kierunek zaś rozumieć należy, by jak najwięcej molekuł, przyśpieszanych za sprawą reakcji chemicznej w silniku, opuściło jego dyszę po trajektorii równoległej do długiej osi rakiety.
Innymi słowy, dążeniem inżynierów jest, by cały gaz, opuszczający dyszę silnika, przybrał kształt prostej „kolumny” pod rakietą.
Sytuacja optymalna: ciśnienie gazów wylotowych równe otoczeniu.
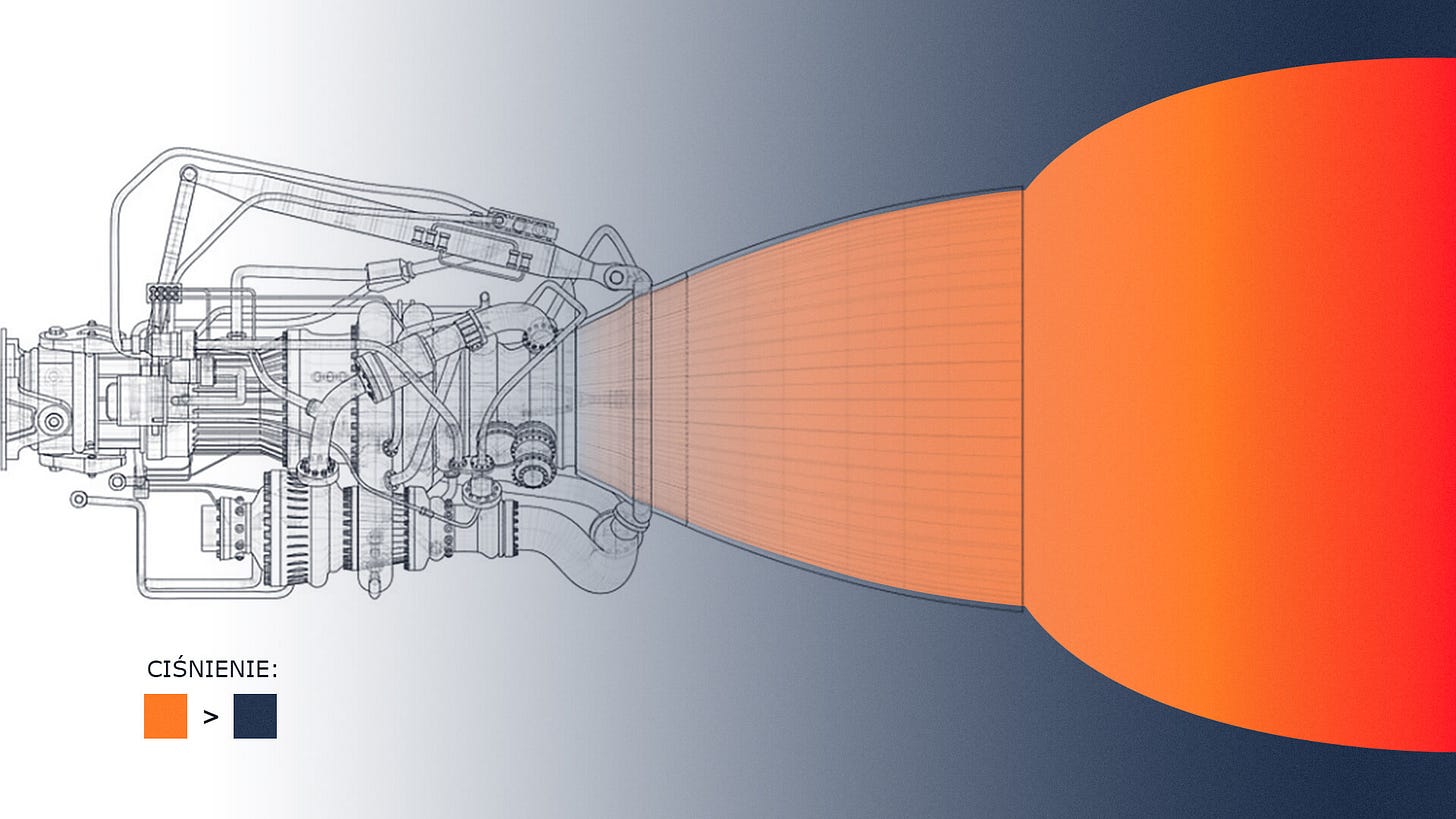
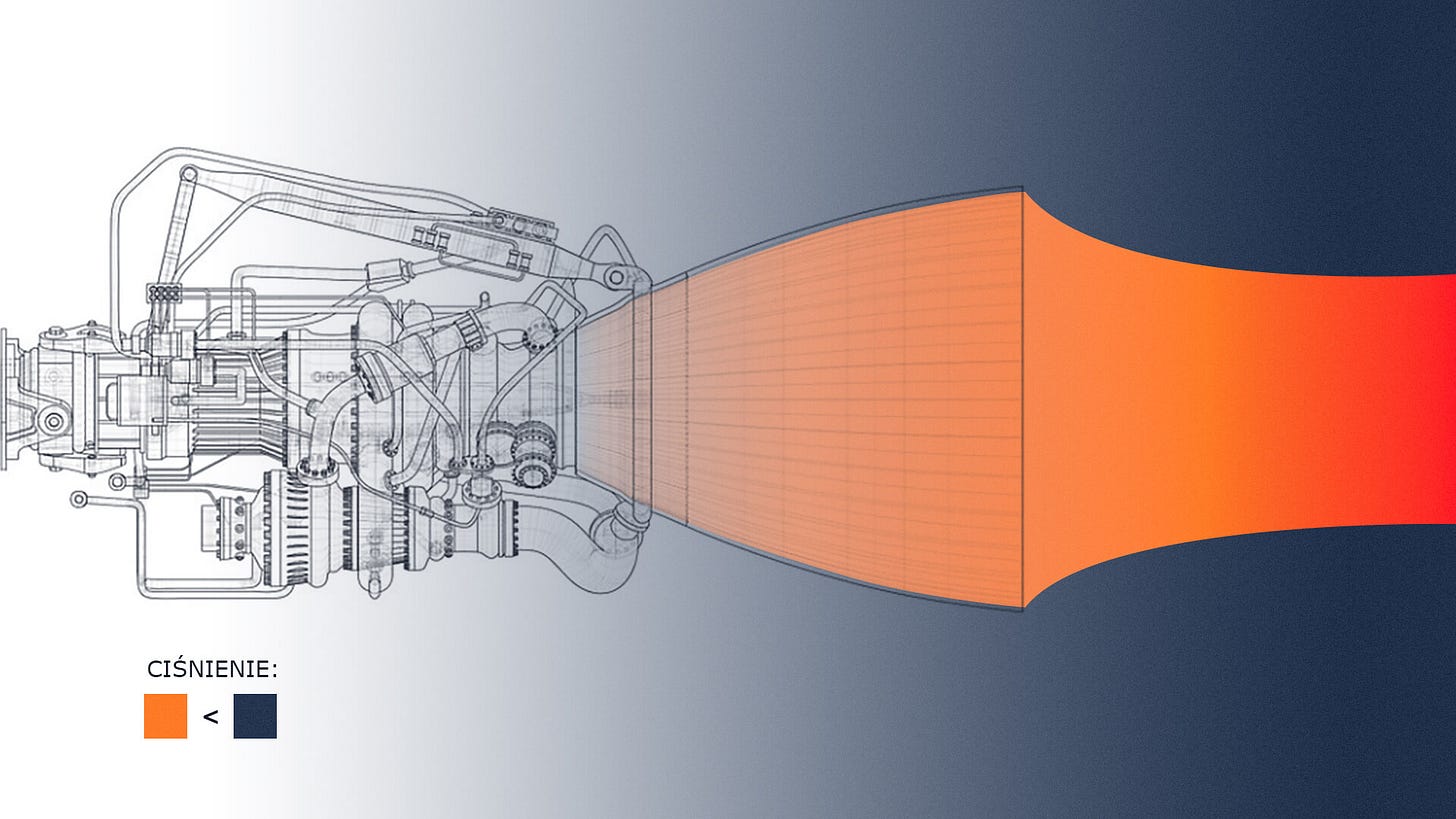
W praktyce jednak, perfekcyjna kolumna nie jest możliwa do uzyskania, ponieważ strumień gazów napotyka ośrodek o zmiennym ciśnieniu: na poziomie gruntu ciśnienie powietrza jest najwyższe, zaś wraz z pokonywaniem kolejnych warstw atmosfery zmierza w stronę zera.
W idealnych warunkach, kształt dyszy zostałby dobrany w tak, by gorący gaz miał w momencie opuszczenia sinika takie samo ciśnienie, jak otoczenie. W warunkach nie-idealnych (czyli każdych rzeczywistych), kolumna ulega albo rozszerzeniu (gdy przestaje być „trzymana w ryzach” przez dyszę, a ciśnienie otoczenia jest niższe niż u jej wylotu), albo „ściśnięciu” przez napierającą atmosferę.
Ostatnia grafika obrazuje niepożądane zjawisko separacji strumienia (ang. flow separation) od ściany dyszy – turbulencje nim spowodowane mogą w skrajnych przypadkach prowadzić nawet do destrukcji silnika.
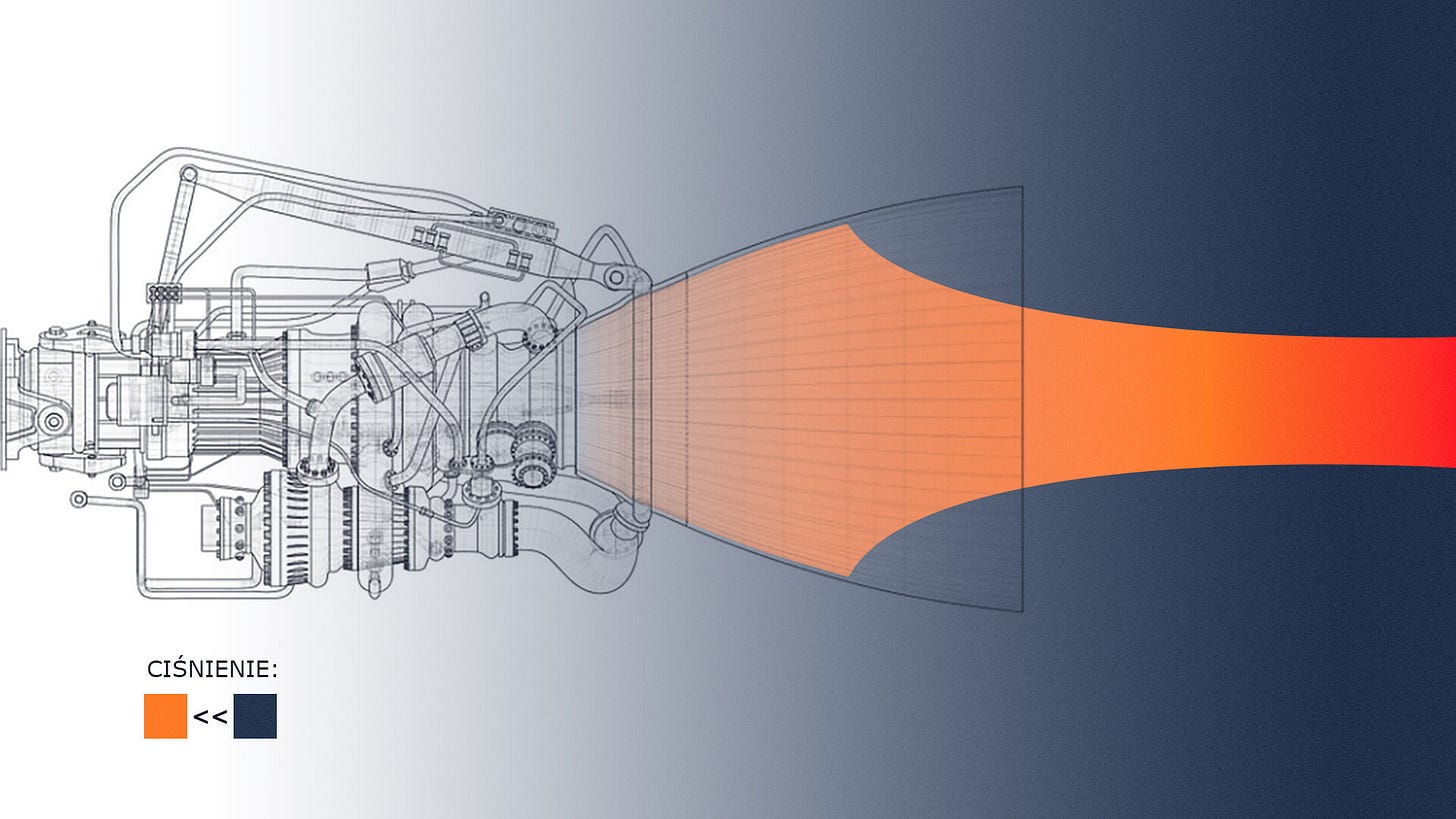
Kształt dyszy projektowany jest więc tak, by zapewniał najbliższy optymalnemu przepływ gazów w całym zakresie pracy silnika. W przypadku Starshipa zwykło się mówić o Raptorach sea-level (pracujących od poziomu morza, tj. najwyższego ciśnienia atmosferycznego, do ich wyłączenia) oraz tzw. Raptorach próżniowych, charakteryzujących się znacznie większą dyszą, zoptymalizowanych do pracy w przestrzeni kosmicznej (nie miały one jeszcze okazji napędzić statku – do tej pory wszystkie testy Starshipa odbywały się w atmosferze; więcej na ten temat w moich artykułach, np. tu lub tu).
Jakkolwiek silniki sea-level mogą być z powodzeniem odpalone w próżni (nie jest wykluczone, że tak właśnie będzie lądować na Księżycu Starship w wersji HLS – uzasadnieniem tych spekulacji jest fakt, że wg obecnego projektu Raptory próżniowe nie są wyposażone w funkcję sterowania wektorem ciągu), ich efektywność będzie znacznie obniżona, ponieważ strumień gazów ulegnie dużej „dekompresji”, tj. cząstki po opuszczeniu dyszy „uciekną na boki”, przez co generowany przez nie ciąg będzie mniejszy. Co prawda, by ww. zjawisko nie wystąpiło wcale, w przypadku silnika pracującego w warunkach zerowego ciśnienia, rozmiar jego dyszy powinien zmierzać ku nieskończoności. Naturalnie, istnieją praktyczne limity, wyznaczające racjonalny rozmiar dyszy (w tym oczywisty: zysk na efektywności silnika ma sens jedynie do momentu, w którym zostaje w pełni zniwelowany przez dodatkową wagę powiększonej dyszy).
Impuls właściwy mierzy właśnie efektywność, z jaką silnik jest w stanie przekształcić dostępne mu paliwo na ciąg. Im większy impuls właściwy (ang. specific impulse), tym mniej paliwa statek potrzebuje do wykonania manewru.
Wartość ta nie informujenas jednak o czasie jego wykonania, tj. o tym, jak długo silnik musi generować ciąg w celu uzyskania pożądanego delta-v. Może to dezorientować, zważywszy na fakt, że wartość impulsu właściwego zwykło się podawać w sekundach (nie występuje dzięki temu potrzeba konwersji jednostek – masa może być mierzona w kilogramach/funtach, odległość w metrach/stopach, jednak miarą czasu niezmiennie pozostaje sekunda; historycznie miało to spore znaczenie dla wygody współpracy między użytkownikami systemu metrycznego i imperialnego).
Jak zatem czytać efektywność silnika podawaną w sekundach?
Wyobraźmy sobie silnik zdolny do wytworzenia 100 ton ciągu – wartość ISP będzie w nim oznaczać, ile sekund może on pracować, zanim zużyje 100 ton paliwa. Jeśli taki silnik osiąga ISP równe x sekund, to silnik o ISP równym 2x sekund będzie spalać paliwo dwukrotnie wolniej, przez cały czas zapewniając ten sam ciąg.
Przeprowadźmy więc prosty eksperyment myślowy – jego przedmiotem będzie hipotetyczny silnik, wykorzystujący najbardziej efektywne, znane nauce paliwo: antymaterię. Impuls właściwy przyjmuje w nim astronomiczne wartości, rzędy wielkości powyżej najdoskonalszego silnika na paliwo chemiczne. Załóżmy, że może on generować maksymalny ciąg 100 kilogramów nieprzerwanie przez lata, co pozwala na rozpędzenie niewielkiego statku kosmicznego do prędkości relatywistycznych. Wyobraźmy sobie następnie, że instalujemy ten cud techniki, zamiast Raptorów, do Starshipa, stojącego na stanowisku startowym. Rzecz jasna, Starship nie podniesie się z platformy nawet o milimetr, choćby nasz silnik na antymaterię pracował 10 lat. Dlaczego? Ponieważ Starship waży na Ziemi więcej niż 100 kilogramów.
Zatem wartość impulsu właściwego (efektywność silnika), a także sumaryczna delta-v, jaką silnik mógłby hipotetycznie wygenerować, same w sobie nie pozwalają na wyciągnięcie wniosków na temat jego przydatności do wysłania rakiety gdziekolwiek.
Stosunek ciągu do masy (TWR)
Równie ważne jest bowiem, jaki ciąg silnik może wygenerować w jednostce czasu – parametr ten ma kluczowe znaczenie, zarówno dla „przełamania” grawitacyjnego wpływu danego ciała (np. startu z Ziemi) jak i dla możliwości efektywnego nawigowania w przestrzeni kosmicznej (zmiana jednej stabilnej orbity na drugą).
Musimy więc wprowadzić kolejne kryterium, a mianowicie momentalny stosunek ciągu do masy (ang. thrust-weight ratio) – mówić możemy zarówno o TWR dla konkretnego silnika jak i całego systemu2.
By rakieta mogła oderwać się od ziemi, wartość współczynnika ciągu do masy musi wynosić powyżej 1.
Oznacza to, że rakieta o masie jednej tony musi wygenerować w danej chwili więcej niż 1000 kg ciągu, by ruszyć z miejsca. Następnie, współczynnik TWR musi zostać utrzymany >1 (w praktyce znacznie powyżej, ponieważ startująca rakieta „walczy” również z tarciem atmosferycznym), aż do osiągnięcia pierwszej prędkości kosmicznej.
Jeżeli ładunek (czyli niewielki ułamek masy całego systemu orbitalnego) nie osiągnie tej prędkości w kierunku prostopadłym do działania siły ciążenia (orbita kołowa), zostanie ponownie ściągnięty na Ziemię.
Na marginesie…
Lubisz poszerzać swoją wiedzę? Być może spodoba Ci się też mój wcześniejszy wpis, będący przystępnym wprowadzeniem do problematyki promieniowania kosmicznego oraz jego znaczenia dla powodzenia misji załogowych na Marsa.
Sugeruję też podać maila Substackowi, dzięki czemu wesprzesz rozwój platformy i otrzymasz rekomendacje ciekawych artykułów od niezależnych twórców, dziennikarzy, popularyzatorów nauki i nie tylko.
Już subskrybujesz? Rozważ udostępnienie moich artykułów na kanałach społecznościowych lub poleć ich lekturę osobie, dla której mogą one być, w Twojej ocenie, interesujące – będzie to dla mnie najlepsza forma podziękowania.
Kalkulując budżet delta-v od samego startu (alternatywą byłoby np. liczenie od uzupełnienia paliwa na orbicie – z takim założeniem projektowany jest Starship), istotne jest ile czasu rakieta potrzebuje do pokonania siły ciążenia – im dłużej uwalnia się ona od groźby ściągnięcia ponownie na Ziemię, tym więcej paliwa spalane jest nieefektywnie (pierwsze 1 g3 przyśpieszenia „marnowane” jest na zrównoważenie siły ciążenia). Jest to tzw. strata na skutek grawitacji – by była ona jak najmniejsza, należy wytworzyć potrzebny do osiągnięcia orbity ciąg w możliwie najkrótszym czasie.
Co ważne, rozpędzony do prędkości orbitalnej obiekt (np. satelita) wciąż znajduje się w stanie permanentnego spadku w kierunku Ziemi, lecz za sprawą jego ruchu równoległego względem zakrzywionej powierzchni planety, nigdy w nią „nie trafia”.
Więcej: każde ciało niebieskie i każdy obiekt, który nie posiada własnego napędu, pozostaje w przestrzeni kosmicznej w stanie swobodnego spadku. Można powiedzieć, że spadek jest w całym kosmosie stanem domyślnym – zmienia się jedynie kierunek (na co spadam) i prędkość spadania (jak bardzo przyśpiesza mnie grawitacja ciała, na które spadam). Księżyc spada na Ziemię (ale nigdy nie spadnie), planety spadają na Słońce. Sonda w drodze na Marsa spada na Słońce aż do momentu, w którym zbliża się do Marsa na tyle, by zacząć spadać na niego.
Często sama koncepcja orbitowania, np. Międzynarodowej Stacji Kosmicznej wokół Ziemi, jest rozumiana błędnie. Wiele (być może wręcz większość) „zaczepionych na ulicy” osób, gdyby poprosić je o wytłumaczenie, dlaczego astronauci nie odczuwają w kosmosie ciążenia, odpowiedziałoby, iż od pewnej wysokości ziemska grawitacja po prostu przestaje oddziaływać na obiekty w kosmosie. Tymczasem, siła grawitacji Ziemi na wysokości orbity ISS jest niemalże taka sama4, jak przy samej jej powierzchni (stacja orbituje bowiem bardzo nisko, jeśli za punkt odniesienia przyjmiemy promień planety).
Stan nieważkości na stacji kosmicznej nie różni się właściwie od tego, jakiego doświadczają pasażerowie spadającego bezwładnie samolotu – z tym tylko, że pikujący w dół samolot ostatecznie roztrzaska się o ziemię, a orbitująca stacja nie przestaje spadać, ponieważ zakrzywiająca się „w dół” powierzchnia Ziemi stale spod niej „ucieka”.
Jak łatwo sobie wyobrazić, by Ziemia uciekała (przez fakt swojej krzywizny) spod spadającego obiektu na tyle szybko, by ten nigdy nie spadł, obiekt ten musi poruszać się z bardzo dużą prędkością „poziomą” – w przypadku naszej planety jest to około 27 tys. km/h (minimalna prędkość orbitalna, czyli tzw. pierwsza prędkość kosmiczna jest charakterystyczna dla każdego ciała niebieskiego). Istotne jest zrozumienie, iż rozpędzenie statku do takiej prędkości w ziemskiej atmosferze byłoby praktycznie niemożliwe, z uwagi na tarcie o cząsteczki powietrza – stąd rakiety lecą najpierw w górę, by „uwolnić” się od spowalniającej je atmosfery jak najszybciej.
Możemy tu wrócić do delta-v i odnotować, że w warunkach braku atmosfery, przyjmuje ona tę samą wartość dla zmian orbity niezależnie od kierunku (zmiana z orbity niższej na wyższą i vice versa).
Czy jednak przyśpieszanie i zwalnianie w przestrzeni kosmicznej zawsze muszą wiązać się ze zużyciem paliwa?
Manewrowanie bez spalania
(czyli spadanie do celu, jak mawiał słynny astronauta Buzz Astral)
Fizycy już od ponad stu lat wiedzą, że przyśpieszenie grawitacyjne (spadek w kierunku środka układu grawitacyjnego) jest nieodróżnialne od przyśpieszenia ogółem. Oznacza to, że astronauta zamknięty w statku i bez wiedzy o parametrach swojego lotu, nie byłby w stanie stwierdzić (niezależnie od tego, jakie eksperymenty przeprowadziłby na pokładzie), czy przyśpiesza ściągany siłą grawitacji czy z wykorzystaniem silnika5.
Wyobraźmy sobie, że chcielibyśmy wysłać sondę tak, aby wleciała prosto w Słońce – mogłoby się wydawać, iż nie powinno to wymagać dużej ilości paliwa: wszak centrum masy całego Układu Słonecznego znajduje się wewnątrz Słońca, więc grawitacja powinna ściągnąć naszą sondę bez problemu. Tymczasem, rozbicie się o Słońce wymaga bardzo dużej delta-v; paradoksalnie znacznie większej niż potrzebnej do wysłania sondy całkowicie poza Układ Słoneczny.
Ten pozornie dziwny fenomen przestaje takim być, gdy uświadomimy sobie konsekwencje, płynące z względności. Sonda nie rozpędza się wszak od zera, a ma pewną niebagatelną prędkość początkową – tyle tylko, że nie względem Ziemi.
Prędkością początkową sondy względem Słońca jest mniej-więcej prędkość orbitalna Ziemi – sonda musiałaby więc najpierw wyhamować (przyśpieszyć w odwrotnym kierunku do ruchu Ziemi po orbicie), tak aby jej nowa trajektoria przecięła tarczę słoneczną. Margines błędu tego manewru byłby stosunkowo niewielki, gdyż zbyt mała zmiana prędkości (wytracenie niewystarczającej części początkowej prędkości orbitalnej) skutkowałaby chybieniem celu: w pierwszej fazie lotu nasza sonda zaczęłaby przyśpieszać grawitacyjnie, spadając na Słonce, by następnie nie trafić w nie i z uzyskaną w „fazie spadania” prędkością zacząć się od niego oddalać, zwalniając (gdyż w tej fazie przyśpieszenie grawitacyjne Słońca miałoby zwrot przeciwny do lotu sondy), aż do ponownego osiągnięcia „wysokości” ziemskiej orbity, mniej-więcej po „drugiej stronie” układu. Sonda znalazłaby się więc na eliptycznej orbicie, wewnątrz dysku orbitalnego Ziemi.
Teoretycznie, możliwe byłoby takie obliczenie trajektorii sondy, by ta przeleciała „w fazie zwalniania” na tyle blisko np. Wenus, by wpływ grawitacji planety na jej lot przeważył wpływ Słońca. Taki manewr byłby tzw. asystą grawitacyjną – pozwala ona skierować statek kosmiczny na inny kurs, bez zużywania paliwa. Co więcej, jeśli planeta używana do takiej asysty posiada atmosferę, można dodatkowo wykorzystać ją do kontrolowanego wytracenia prędkości (niezależnie od tego, czy zamierzamy na danej planecie lądować). I choć rozpocząłem akapit słowem teoretycznie, opisywana sytuacja nie jest bynajmniej czystą teorią – patrz video na końcu artykułu.
Misje z reguły planowane są tak, by w jak największym stopniu wytracać prędkość dzięki atmosferycznemu tarciu u celu podróży (albo po drodze), nie przez zużywanie paliwa w przestrzeni międzyplanetarnej.
Co ciekawe, umiejętne korzystanie z asysty grawitacyjnej pozwala nie tylko na redukcję, lecz także na zwiększenie prędkości statku.
Fakt ten również ma prawo jawić się jako niemała zagwozdka, nawet dla skądinąd dobrze zorientowanych amatorów fizyki – jak to możliwe, że sonda opuszcza studnię grawitacyjną planety z większą prędkością niż była przez nią przyciągana, bez użycia silnika? Skąd dodatkowa energia?
„Dodatkowej” energii oczywiście nie ma – jeśli sonda ma przyśpieszyć, to coś musi zwolnić. Np. Jowisz czy Saturn. Zwiększenie prędkości z użyciem asysty grawitacyjnej nie byłoby wszak możliwe, gdyby ciało jej udzielające „stało w miejscu” – dlatego manewr ten rozpatrywać należy przede wszystkim w układzie sonda-Słońce. Gdy pominąć Słońce jako punkt odniesienia, sonda nie oddala się od planety szybciej. Jednak mierząc jej prędkość względem centrum Układu Słonecznego, może ona zyskać znaczną prędkość, „nurkując” niejako „za” asystującą planetą i korzystając z jej ruchu orbitalnego (a ten jest stosunkowo szybki, Jowisz np. pokonuje w sekundę około 13 km po swojej orbicie wokół Słońca; Ziemia 30 km).
Dobrym porównaniem jest deskorolkarz, który chcąc nabrać prędkości chwyta się przejeżdżającego samochodu. Co ważne, jego manewr niezauważalnie spowalnia samochód – tak samo, jak rozpędzająca się „na gapę” sonda zabiera planecie część jej pędu (przy czym „strata” po stronie planety jest dosłownie niemierzalna, zważywszy na proporcje mas).
Starannie planując misję, można skorzystać z wielu asyst grawitacyjnych – manewrowanie tą metodą (pomijając konieczność precyzyjnych korekt kursu) nie konsumuje „zapasu” delta-v, jakim dysponuje statek.
Niektóre z możliwych scenariuszy wpływu grawitacji planety na zmianę orbity przelatującej sondy [Twórca GIFa: David Shortt; uwaga: jest on rownież autorem świetnego artykułu, w którym zasady rządzące asystami grawitacyjnymi zostały opisane znacznie bardziej szczegółowo – polecam.]
Wciąż nie do końca jasne? Nie wahaj się sformułować pytania w komentarzu. Skomentuj tym bardziej, jeśli uważasz, że moje wyjaśnienie może wprowadzać kogoś w błąd. Konstruktywna krytyka jest tu bardzo mile widziana:)
Jakkolwiek skrupulatne planowanie pozwala na „ekonomiczne” przemieszczanie się między dowolnymi planetami, podejście to ma zasadniczą wadę w kontekście statków z ludźmi na pokładzie (przynajmniej do czasu wynalezienia hibernacji, znanej doskonale z domeny s-f). Wybieranie „okrężnych tras” nie jest zbyt praktyczne, jeśli lot ma przez to trwać kilka lat dłużej6.
Na atrakcyjne położenie planet warto jednak czekać – dzięki zdarzającemu się raz na 176 lat układowi, sonda Voyager 2 zdołała okraść z prędkości orbitalnej wszystkie cztery gazowe olbrzymy, co pozwoliło jej zostawić w tyle Układ Słoneczny7. Nadanie Voyagerom prędkości ucieczki ze studni grawitacyjnej Słońca było ówcześnie niemożliwe wyłącznie z użyciem ciągu silników – już pierwsza asysta Voyagera 2 zapewniła mu ponad dwukrotne zwiększenie prędkości (licząc z heliocentrycznego punktu odniesienia, oczywiście).
Odnotujmy w tym miejscu, że absolutnie nic nie stoi na przeszkodzie, by jeden statek „okradał” daną planetę wielokrotnie, jak Cassini w drodze na orbitę Saturna:
A skoro o wielokrotnym wykorzystaniu Wenus mowa, nie sposób nie wspomnieć o sondzie Parker – by osiągnąć cel w postaci rekordowego zbliżenia się do Słońca, sonda konsekwentnie wytraca prędkość, nadaną jej początkowo przez Ziemię. Każda z siedmiu asyst grawitacyjnych Wenus „zwęża” słoneczną orbitę statku (staje się ona bardziej eliptyczna), aż do osiągnięcia trajektorii docelowej w roku 2024 (video poniżej). Pozwoli ona Parkerowi zbliżyć się do naszej gwiazdy zaledwie na 10-krotność jej promienia. Ściągana grawitacją Słońca, sonda będzie wtedy najszybszym wytworem technologii w historii, rozpędzając się do około 700 000 km na godzinę (200 km/s).
Na marginesie…
Artykuł jest uzupełnieniem mojego cyklu edukacyjnego, w którym staram się przybliżać skomplikowane zagadnienia kosmiczne możliwie nieskomplikowanym językiem.
Z reguły pracuję przy dobrej kawie, dlatego jeśli chcesz zmotywować mnie do pisania i tym samym przyczynić się do popularyzacji wysokiej jakości, pozbawionej reklam treści w Internecie, rozważ postawienie mi następnej filiżanki:
(rejestracja w serwisie BuyCoffee nie jest wymagana)
Z góry dziękuję:)
PS. Fundamentalną dla mnie sprawą jest jednak, by pewna rzecz była jasna: jeśli zastanawiasz się od czasu do czasu, czy stać Cię na latte z pianką, czy może lepiej odmówić sobie wyjścia do kawiarni i zamiast tego opłacić Netflix w terminie, akapit powyżej nie jest adresowany do Ciebie – nie chciałbym wywołać poczucia, że wywierana jest na Tobie jakakolwiek presja. Moje artykuły, w których omawiam zagadnienia związane z eksploracją kosmosu są i będą dostępne bezpłatnie.
Jeżeli natomiast obce są Tobie dylematy z kategorii Netflix czy Starbucks, a chcesz docenić czas, jaki został włożony w tworzenie dostępnych tu wpisów, link wyżej pozwoli Ci na sprezentowanie mi kawy BLIKiem lub inną, preferowaną metodą.
Przykładowo, thrust-weight ratio silnika Merlin to około 180, a całej rakiety Falcon 9 (w momencie startu, gdy jest najcięższa) około 1.3-1.4. Dla porównania, opuszczającego platformę startową Starshipa, choć będzie to zdecydowanie najcięższy obiekt, jaki kiedykolwiek uniósł się z Ziemi, ma docelowo cechować TWR na poziomie powyżej 1.5 – innymi słowy, rakieta wystartuje bardziej dynamicznie niż wielokrotnie lżejszy Falcon (stanie się to możliwe dzięki potężnemu ciągowi, generowanemu przez 33 silniki Raptor 2).
Grawitacja Ziemi przyciąga wszystkie obiekty w jej kierunku, przyśpieszając je tym bardziej, im bliżej się znajdują – przy powierzchni wartość tego przyśpieszenia to niecałe 10 m/s², czyli 1 g (standardowe ciążenie). Oznacza to, że rakieta zdolna przyśpieszać 15 m/s² w warunkach braku ciążenia, startując z Ziemi osiągnie jedynie 5 m/s² maksymalnego przyśpieszenia w pionie.
Nie dotyczy generowania sztucznej grawitacji z pomocą ruchu wirowego – ten da się odróżnić od „prawdziwej” grawitacji nawet w zamkniętym układzie odniesienia.
Dlatego właśnie „nadwyżki” delta-v,jakie może potencjalnie osiągnąć Starship, jawią się jako game changer dla całego prospektu załogowej eksploracji kosmosu.
Siostrzana sonda Voyager 1, której misja rozpoczęła się 16 dni później, wyprzedziła Voyagera 2 i jest obecnie najdalszym obiektem stworzonym przez ludzkość, wciąż przesyłając ważne dane naukowe z odległości ponad 21,5 godzin świetlnych… a przynajmniej były to ważne dane naukowe jeszcze do niedawna, gdyż wczoraj NASA poinformowała, że pojawiły się problemy z telemetrią Voyagera. Inżynierowie wciąż diagnozują przyczynę komplikacji – w oświadczeniu NASA JPL czytamy, że być może uda się wdrożyć rozwiązanie w postaci aktualizacji oprogramowania sondy, a jeśli powodem kłopotów jest hardware (wszak ma on już blisko 45 lat), zostanie zbadana opcja wykorzystania komponentów zapasowych (nie byłby to pierwszy raz – 5 lat temu Voyager 1 został przełączony na „zapasowe” dysze manewrujące, by móc wciąż utrzymywać właściwą orientację względem Ziemi, pozwalającą na odbieranie sygnału).
